Heap
Heap is an important data structure and is the preferred data structure for implementing Priority Queues. Since there are many variants of the heap, including the binomial heap, the Fibonacci heap, etc., only the most common one is the binary heap (hereinafter referred to as the heap).
A heap is a binary tree that satisfies a certain nature. The concrete heap has the following properties: the key value of the parent node is always not greater than the key value of its child node (small top heap), and the heap can be divided into small top heap and large top. Heap, here is a small top heap, for example, its main operations are:
Insert()
extractMin
Peek(findMin)
Delete(i)
Since the heap is a morphological rule binary tree, the parent node of the heap has the following relationship with the child node:
If the number of the parent node is i, the number of the left child node is 2*i+1, and the number of the right child node is 2*i+2. If the number of the child node is i, the number of the parent node is (i) -1)/2
Since the good shape of the binary tree already contains the relationship information between the parent node and the child node, it is possible to simply use the array to store the heap without using a linked list.
To implement the basic operations of the heap, the two key functions involved
siftUp(i, x) : Adjusts the element x of position i upwards to satisfy the heap nature, often used after inserts to adjust the heap;
siftDown(i, x): For the same reason, often used for adjusting heap after delete(i);
The specific operations are as follows:
privatevoidsiftUp(inti){
Intkey = nums[i];
For(;i > 0;){
Intp = (i - 1) >>> 1;
If(nums[p] <= key)
Break;
Nums[i] = nums[p];
i = p;
}
Nums[i] = key;
}
privatevoidsiftDown(inti){
Intkey = nums[i];
For(;i < nums.length / 2;){
Intchild = (i << 1) + 1;
If(child + 1 < nums.length && nums[child] > nums[child+1])
Child++;
If(key <= nums[child])
Break;
Nums[i] = nums[child];
i = child;
}
Nums[i] = key;
}
You can see that siftUp and siftDown are constantly comparing and exchanging between the parent node and the child node; you can complete the operation without exceeding the logn time complexity.
With these two basic functions, you can implement the basic operations of the heap mentioned above.
The first is how to build a heap, there are two ideas for building a heap:
One is constantly insert (siftUp is called after insert)
The other treats the original array as a heap that needs to be adjusted, and then calls siftDown(i) from bottom to bottom at each position i. Upon completion, we get a heap that satisfies the nature of the heap. Consider the latter idea here:
Usually the heap insert operation is to insert the element into the end of the heap. Since the insertion of the new element may violate the nature of the heap, you need to call the siftUp operation to adjust the heap from the bottom up; the heap removes the top element element is to delete the top element, then Putting the last element of the heap on top of the heap, and then performing the siftDown operation, the same is true for replacing the top element of the heap.
Building
// Create a small top heap
privatevoidbuildMinHeap(int[]nums){
Intsize = nums.length;
For(intj = size / 2 - 1;j >= 0;j--)
siftDown(nums,j,size);
}
So what is the time complexity of the build operation? The answer is O(n). Although the operation time of siftDown is logn, since the height is decreasing, the number of nodes in each layer is also reduced by multiple times. Finally, the time complexity is O(n) by subtracting the series of misalignments.
extractMin due to the inherent nature of the heap, the root of the heap is the smallest element, so the peek operation is to return the root nums[0] element; to delete nums[0], you can end the element nums[n-1] Override nums[0], then heap size = size-1, call siftDown(0) to adjust the heap. The time complexity is logn.
Peek ibid
Delete(i)
Delete the node in position i, involving two functions siftUp and siftDown, the time complexity is logn, the specific step is
Overwrite element i with element last, then siftDown
Check if you need siftUp
Note that the heap delete operation, if you delete the root node of the heap, you do not need to consider the operation of siftUp; if you delete the non-root node of the heap, depending on the situation, it is siftDown or siftUp operation, the two operations are mutually exclusive of.
Publicintdelete(inti){
Intkey = nums[i];
/ / Move the last element, first siftDown; depending on the situation, consider whether siftUp
Intlast = nums[i] = nums[size-1];
Size--;
siftDown(i);
//check #i's node key value does change (if siftDown operation takes effect), if it changes, ok, otherwise to ensure heap nature, you need siftUp
If(i < size && nums[i] == last){
System.out.println("delete siftUp");
siftUp(i);
}
Returnkey;
}
Case 1 :
Delete the intermediate node i21 and copy the last node;

Since the siftDown operation is not performed, the value of node i is still 6, so to ensure the nature of the heap, the siftUp operation is performed;
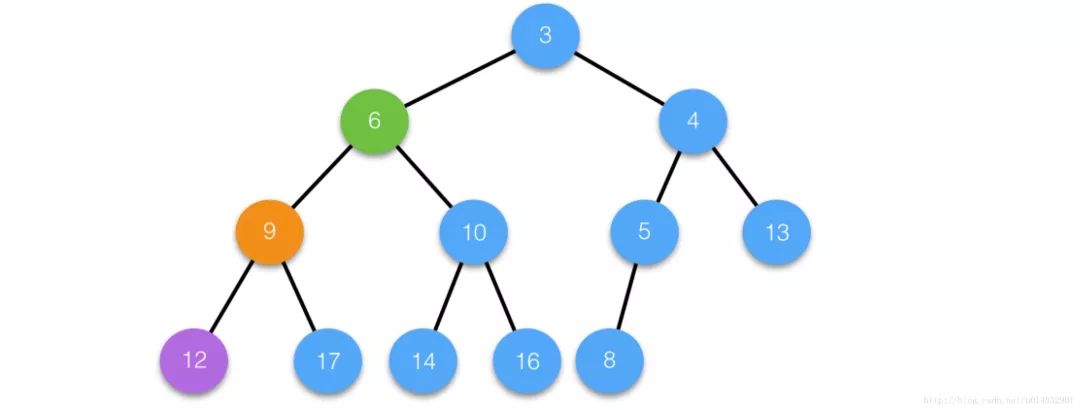
Case 2
Delete the intermediate node i, copy the node with the value of 11 and execute the siftDown operation.
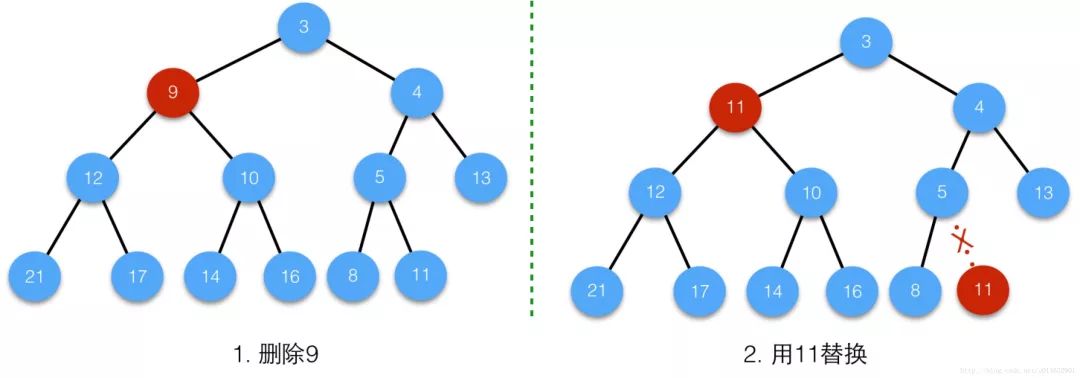
Since the value of node i is no longer 11 after the siftDown operation, there is no need to perform the siftUp operation because the nature of the heap has been maintained after the siftDown operation takes effect.

It can be seen that the basic operation of the heap depends on the two core functions siftUp and siftDown; the more complete Heap code is as follows:
classHeap{
privatefinalstaticintN = 100;//default size
Privateint[]nums;
Privateintsize;
publicHeap(int[]nums){
This.nums = nums;
This.size = nums.length;
Heapify(this.nums);
}
publicHeap(){
This.nums = newint[N];
}
/**
* heapify an array, O(n)
* @param nums An array to be heapified.
*/
Privatevoidheapify(int[]nums){
For(intj = (size - 1) >> 1;j >= 0;j--)
siftDown(j);
}
/**
* append x to heap
* O(logn)
* @param x
* @return
*/
Publicintinsert(intx){
If(size >= this.nums.length)
expandSpace();
Size += 1;
Nums[size-1] = x;
siftUp(size-1);
Returnx;
}
/**
* delete an element located in i position.
* O(logn)
* @param i
* @return
*/
Publicintdelete(inti){
rangeCheck(i);
Intkey = nums[i];
/ / Overlay the last element, first siftDown; depending on the situation, consider whether siftUp;
Intlast = nums[i] = nums[size-1];
Size--;
siftDown(i);
//check #i's node key value does change, if it changes, then ok, otherwise to ensure the heap nature, you need siftUp;
If(i < size && nums[i] == last)
siftUp(i);
Returnkey;
}
/**
* remove the root of heap, return it's value, and adjust heap to maintain the heap's property.
* O(logn)
* @return
*/
publicintextractMin(){
rangeCheck(0);
Intkey = nums[0],last = nums[size-1];
Nums[0] = last;
Size--;
siftDown(0);
Returnkey;
}
/**
* return an element's index, if not exists, return -1;
* O(n)
* @param x
* @return
*/
Publicintsearch(intx){
For(inti = 0;i < size;i++)
If(nums[i] == x)
Returni;
Return -1;
}
/**
* return but does not remove the root of heap.
* O(1)
* @return
*/
Publicintpeek(){
rangeCheck(0);
Returnnums[0];
}
privatevoidsiftUp(inti){
Intkey = nums[i];
For(;i > 0;){
Intp = (i - 1) >>> 1;
If(nums[p] <= key)
Break;
Nums[i] = nums[p];
i = p;
}
Nums[i] = key;
}
privatevoidsiftDown(inti){
Intkey = nums[i];
For(;i < size / 2;){
Intchild = (i << 1) + 1;
If(child + 1 < size && nums[child] > nums[child+1])
Child++;
If(key <= nums[child])
Break;
Nums[i] = nums[child];
i = child;
}
Nums[i] = key;
}
privatevoidrangeCheck(inti){
If(!(0 <= i && i < size))
thrownewRuntimeException("Index is out of boundary");
}
privatevoidexpandSpace(){
This.nums = Arrays.copyOf(this.nums,size *2);
}
publicStringtoString(){
// TODO Auto-generated method stub
StringBuilder sb = newStringBuilder();
Sb.append("[");
For(inti = 0;i < size;i++)
Sb.append(String.format((i != 0?", " : "") + "%d",nums[i]));
Sb.append("] ");
returnsb.toString();
}
}
2. Heap application: heap sorting
Using the nature of the heap, we can get a common, stable, and efficient sorting algorithm -- heap sorting. The time complexity of heap sorting is O(n*log(n)), and the space complexity is O(1). The idea of ​​heap sorting is: build a heap for unordered array nums with n elements (here is small) Top heap) heap, then execute extractMin to get the smallest element, so executing n times to get the sequence is the sorted sequence. If it is in descending order, it is a small top heap; otherwise, it uses a large top heap.
Trick
Since the last element last has been moved to root after extractMin is executed, the element returned by extractMin can be placed at the end, so that the heap sorting algorithm of sort in place can be obtained.
The specific operations are as follows:
Int[]n = newint[]{1,9,5,6,8,3,1,2,5,9,86};
Heaph = newHeap(n);
For(inti = 0;i < n.length;i++)
n[n.length-1-i] = h.extractMin();
Of course, if you don't use the previously defined heap, you can manually write the heap sort. Since the heap sorting design is built into the build and extractMin, both operations depend on the siftDown function publicly, so we only need to implement siftDown. (trick: Since the build operation can use siftUp or siftDown, and extractMin requires siftDown operation, so take the public part, use siftDown to build the heap).
This is convenient to be unified with the front, using a small top heap array for descending order.
publicvoidheapSort(int[]nums){
Intsize = nums.length;
buildMinHeap(nums);
While(size != 0){
// swap the top and last element
Inttmp = nums[0];
Nums[0] = nums[size - 1];
Nums[size - 1] = tmp;
Size--;
siftDown(nums,0,size);
}
}
// Create a small top heap
privatevoidbuildMinHeap(int[]nums){
Intsize = nums.length;
For(intj = size / 2 - 1;j >= 0;j--)
siftDown(nums,j,size);
}
privatevoidsiftDown(int[]nums,inti,intnewSize){
Intkey = nums[i];
While(i < newSize >>> 1){
intleftChild = (i << 1) + 1;
intrightChild = leftChild + 1;
// The youngest child is smaller than the youngest child
Intmin = (rightChild >= newSize || nums[leftChild] < nums[rightChild])?leftChild : rightChild;
If(key <= nums[min])
Break;
Nums[i] = nums[min];
i = min;
}
Nums[i] = key;
}
3. Heap application: priority queue
The priority queue is an abstract data type. Its relationship with the heap is similar. List has the same relationship with arrays and linked lists. We often use heaps to implement priority queues. Therefore, many times the heap and priority queues are similar, they are just concepts. The distinction on the top. The application scenarios of priority queues are very extensive: common applications are:
Dijkstra's algorithm (the single source shortest path problem needs to find the shortest adjacency edge of a point in the adjacency list, which can reduce the complexity.)
Huffman coding (a typical example of a greedy algorithm that uses a priority queue to build an optimal prefix encoding tree (prefixEncodeTree))
Prim's algorithm for minimum spanning tree
Best-first search algorithms
Here is a brief introduction to one of the above applications: Huffman coding.
Huffman coding is a variable length coding scheme. For each character, the length of the corresponding binary bit string is inconsistent, but the following principles are observed:
The length of the binary bit string of the character with high frequency is small
The binary bit string s where there is no character c is the prefix of the binary bit string of any character except c
Huffman coding that adheres to such a principle is variable-length coding, which can compress data without loss. After compression, it usually saves 20%-90% of space. The specific compression ratio depends on the inherent structure of the data.
The implementation of Huffman coding is to find the character-binary string comparison relationship that satisfies these two principles, that is, the coding scheme for finding the optimal prefix code (prefix code: the binary bit string without any character encoding is the bit string of other character encoding) Prefix). Here we need to use a binary tree to express the optimal prefix code. This tree is called the optimal prefix code tree. An optimal prefix code tree looks like this:
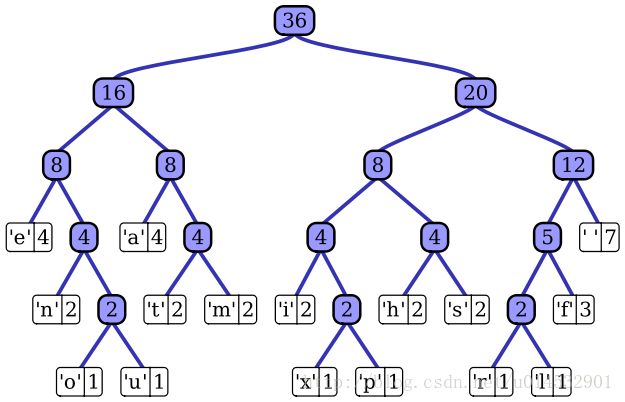
Algorithm idea: Combine the current smallest two elements x, y with a minimum priority queue Q with the attribute freqeunce keyword to get a new element z (z.frequence = x.freqeunce + y.frequence), then insert it into the first priority In Q of the queue, after performing n-1 merges in this way, an optimal prefix code tree is obtained (the proof of the algorithm is not discussed here).
A common build process is as follows:
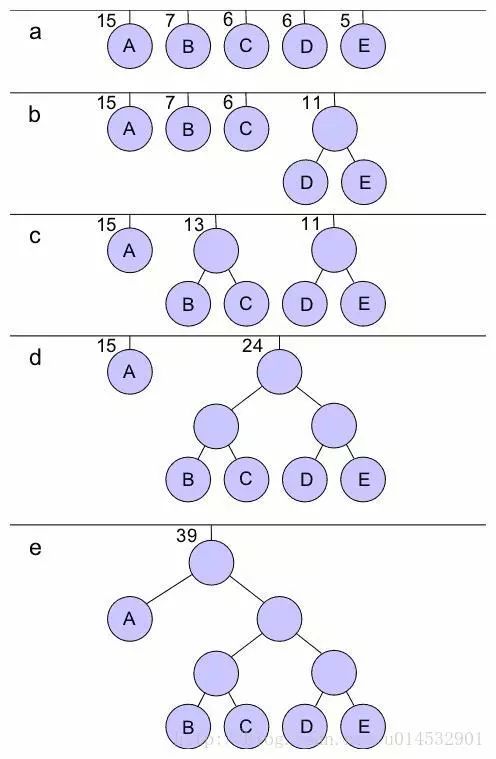
The edge of the child pointing to a node on the left side of the tree represents bit 0, pointing to the representation bit 1 on the edge of the right child, so that a comparison table can be obtained by traversing an optimal prefix code tree.
Import java.util.Comparator;
Import java.util.HashMap;
Import java.util.Map;
Import java.util.PriorityQueue;
/**
*
* root
* /
* --------- ----------
* |c:freq | | c:freq |
* --------- ----------
*
*
*/
publicclassHuffmanEncodeDemo{
Publicstaticvoidmain(String[]args){
// TODO Auto-generated method stub
Node[]n = newNode[6];
Float[]freq = newfloat[]{9,5,45,13,16,12};
Char[]chs = newchar[]{'e','f','a','b','d','c'};
HuffmanEncodeDemo demo = newHuffmanEncodeDemo();
Node root = demo.buildPrefixEncodeTree(n,freq,chs);
Map
StringBuilder sb = newStringBuilder();
demo.tranversalPrefixEncodeTree(root,collector,sb);
System.out.println(collector);
Strings = "abcabcefefefeabcdbebfbebfbabc";
StringBuilder sb1 = newStringBuilder();
For(charc : s.toCharArray()){
Sb1.append(collector.get(c));
}
System.out.println(sb1.toString());
}
publicNode buildPrefixEncodeTree(Node[]n,float[]freq,char[]chs){
PriorityQueue
Publicintcompare(Node o1,Node o2){
Returno1.item.freq > o2.item.freq?1 : o1.item.freq == o2.item.freq?0 : -1;
};
});
Nodee = null;
For(inti = 0;i < chs.length;i++){
n[i] = e = newNode(null,null,newItem(chs[i],freq[i]));
pQ.add(e);
}
For(inti = 0;i < n.length - 1;i++){
Nodex = pQ.poll(), y = pQ.poll();
Nodez = newNode(x,y,newItem('$',x.item.freq + y.item.freq));
pQ.add(z);
}
returnpQ.poll();
}
/**
* tranversal
* @param root
* @param collector
* @param sb
*/
publicvoidtranversalPrefixEncodeTree(Node root,Map
// leaf node
If(root.left == null && root.right == null){
Collector.put(root.item.c,sb.toString());
Return;
}
Node left = root.left,right = root.right;
tranversalPrefixEncodeTree(left,collector,sb.append(0));
Sb.delete(sb.length() - 1, sb.length());
tranversalPrefixEncodeTree(right,collector,sb.append(1));
Sb.delete(sb.length() - 1, sb.length());
}
}
classNode{
PublicNode left,right;
PublicItem item;
publicNode(Node left,Node right,Item item){
Super();
This.left = left;
This.right = right;
This.item = item;
}
}
classItem{
Publiccharc;
Publicfloatfreq;
publicItem(charc,floatfreq){
Super();
This.c = c;
This.freq = freq;
}
}
The output is as follows:
{a=0, b=101, c=100, d=111, e=1101, f=1100}
010110001011001101110011011100110111001101010110011110111011011100101110110111001010101100
4 Heap application: Find the number set of TopK (below 10,000 level) in the massive real number (more than 100 million level).
A: I usually encounter the TopK problem in a collection. The idea is sorting, because common sorting algorithms such as fast counting are faster, and then take K TopK numbers, the time complexity is O(nlogn). When n is very large, the complexity of this time is still very large;
B: Another way of thinking is to break the stage. Each element is compared with K candidate elements once. The time complexity is very high: O(k*n), this scheme is obviously inferior to the former.
For 100 million data, the A scheme is approximately 26.575424*n;
C: Since we only need TopK, we don't need to sort all the data. We can use the idea of ​​heap to maintain a small top heap of size K, and then traverse each element e in turn. If the element e is larger than the top element root, Then delete root, put e at the top of the heap, and then adjust, the time complexity is logK; if less than or equal to, the next element is examined. After traversing this way, the number retained in the smallest heap is the topK we are looking for. The overall time complexity is O(k+n*logk) is approximately equal to O(n*logk), which is approximately 13.287712*n (due to k and n The magnitude difference is too large), so the time complexity has dropped by about half.
Among the three schemes A, B, and C, C is usually better than B because logK is usually smaller than k. The more the magnitude difference between K and n is, the more effective this method is.
The following are specific operations:
Import java.io.File;
Import java.io.FileNotFoundException;
Import java.io.PrintWriter;
Import java.io.UnsupportedEncodingException;
Import java.util.Arrays;
Import java.util.Scanner;
Import java.util.Set;
Import java.util.TreeSet;
publicclassTopKNumbersInMassiveNumbersDemo{
Publicstaticvoidmain(String[]args){
// TODO Auto-generated method stub
Int[]topK = newint[]{50001,50002,50003,50004,50005};
genData(1000 * 1000 * 1000,500, topK);
Longt = System.currentTimeMillis();
findTopK(topK.length);
System.out.println(String.format("cost:%fs",(System.currentTimeMillis() - t) * 1.0 / 1000));
}
publicstaticvoidgenData(intN, intmaxRandomNumer, int[]topK){
Filef = newFile("data.txt");
Intk = topK.length;
Set
For(;;){
Index.add((int)(Math.random() * N));
If(index.size() == k)
Break;
}
System.out.println(index);
Intj = 0;
Try{
PrintWriter pW = newPrintWriter(f,"UTF-8");
For(inti = 0;i < N;i++)
If(!index.contains(i))
pW.println((int)(Math.random() * maxRandomNumer));
Else
pW.println(topK[j++]);
pW.flush();
}catch(FileNotFoundExceptione){
// TODO Auto-generated catch block
e.printStackTrace();
}catch(UnsupportedEncodingExceptione){
// TODO Auto-generated catch block
e.printStackTrace();
}
}
publicstaticvoidfindTopK(intk){
Int[]nums = newint[k];
//read
Filef = newFile("data.txt");
Try{
Scanner scanner = newScanner(f);
For(intj = 0;j < k;j++)
Nums[j] = scanner.nextInt();
Heapify(nums);
//core
While(scanner.hasNextInt()){
Inta = scanner.nextInt();
If(a <= nums[0])
Continue;
Else{
Nums[0] = a;
siftDown(0,k,nums);
}
}
System.out.println(Arrays.toString(nums));
}catch(FileNotFoundExceptione){
// TODO Auto-generated catch block
e.printStackTrace();
}
}
//O(n), minimal heap
Publicstaticvoidheapify(int[]nums){
Intsize = nums.length;
For(intj = (size - 1) >> 1;j >= 0;j--)
siftDown(j,size,nums);
}
privatestaticvoidsiftDown(inti, int, int[]nums){
Intkey = nums[i];
For(;i < (n >>> 1);){
Intchild = (i << 1) + 1;
If(child + 1 < n && nums[child] > nums[child+1])
Child++;
If(key <= nums[child])
Break;
Nums[i] = nums[child];
i = child;
}
Nums[i] = key;
}
}
Ps: I have roughly tested it. It takes 140 seconds to find top5 in 1 billion. It should be very fast.
5 Summary
Heaps are tree-based important data structures that satisfy certain constraints. There are many variants such as binary heaps, binomial heaps, Fibonacci heaps (very efficient), and so on.
Several basic operations of the heap rely on two important functions, siftUp and siftDown. The heap insert is usually inserted at the end of the heap and siftUp adjusts the heap, while extractMin removes the top element and then places the last element on the heap. Top and call siftDown to adjust the heap.
A binary heap is a commonly used heap, which is a binary tree; due to the good nature of binary trees, arrays are often used to store heaps. The time complexity of heaping basic operations is shown in the following table:
Heapify insert peek extractMin delete(i)| O(n) | O(logn) | O(1) | O(logn) | O(logn) |
The binary heap is usually used to implement the heap sorting algorithm. The heap sorting can be sorted in place. The upper bound of the time complexity of heap sorting is O(nlogn), which is an excellent sorting algorithm. Since the two elements with the same key value are in two subtrees, and the order of the two elements may change in subsequent heap adjustments, the heap ordering is not stable. Sorting in descending order requires the establishment of a small top heap, and ascending ordering requires the establishment of a large top heap.
Heap is a way to implement priority queues of abstract data types. Priority queues have a wide range of applications. For example, Huffman coding uses priority queues to construct optimal prefix coding trees using greedy algorithms.
Another application of the heap is to find the TopK number in the massive data. The idea is to maintain a binary heap of size K, and then continuously compare the top elements of the heap to determine whether it is necessary to perform the operation of replacing the top element. The time complexity is n*logk, which is a very effective method when the magnitude difference between k and n is large.
6 references
[1] https://en.wikipedia.org/wiki/Heap_(data_structure))
[2] https://en.wikipedia.org/wiki/Heapsort
[3] https://en.wikipedia.org/wiki/Priority_queue
[4] https://
[5] Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivers, Clifford Stein. Introduction to Algorithms [M]. Beijing: Mechanical Industry Press, 2015: 245-249
[6] Jon Bentley. Programming Beads [M]. Beijing: People's Posts and Telecommunications Press, 2015:161-174
â—This article is numbered 591. If you want to read this article, you can enter 591 directly.
â— Enter m to get the article directory
Car Phone Wireless Charging Coil,Circuit Board Induction Coils,Intersection Induction Coils,Induction Coil Set
Shenzhen Sichuangge Magneto-electric Co. , Ltd , https://www.scginductor.com
