BCD code. Binary-Coded Decimal, referred to as BCD, is called BCD code or two-digit decimal code, also known as binary code decimal number. Is a binary digitally encoded form with a binary coded decimal code. This encoding takes advantage of four bits to store a decimal number, allowing fast conversion between binary and decimal. This coding technique is most commonly used in the design of accounting systems because accounting systems often require accurate calculations of very long strings of numbers. Compared with the general floating-point notation method, the BCD code can save the accuracy of the value and eliminate the time taken for the computer to perform floating-point operations. In addition, BCD coding is also very common for other calculations that require high precision.
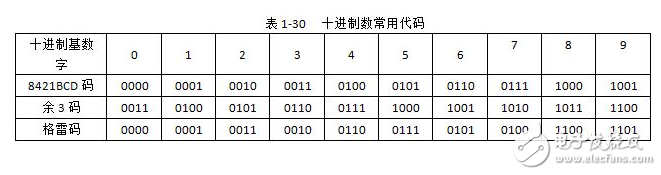
Since decimal numbers have 0, 1, 2, ..., and 9 ten digits, at least 4 binary codes are required to represent a 1-digit decimal number. The 4-digit binary code has 2^4=16 code groups. Among the 16 codes, 10 can be selected to represent 10 decimal numbers, for a total of N=16! /(16-10)! Approximately 10 times the ratio of 2.9 times 10 to 10 squares. Commonly used BCD codes are listed at the end.
BCD code algorithmBCD code operation rules: BCD code is a decimal number, and the operator performs processing on the binary operation rules when adding or subtracting data. Thus, when the BCD code is transmitted to the arithmetic unit for calculation, the result needs to be corrected.
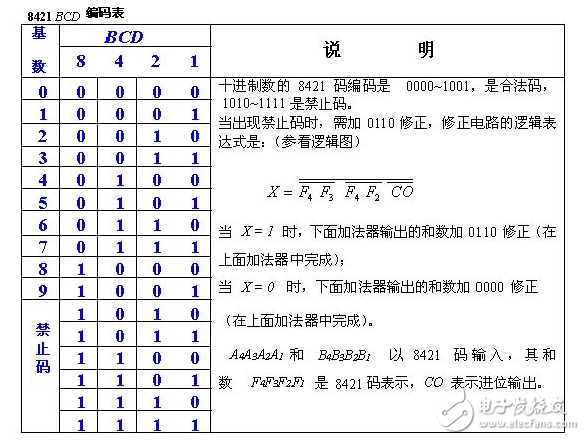
The rule of correction is: when two BCD codes are added, if the sum is equal to or less than 1001 (ie, the decimal number is 9), no correction is needed; if the sum is 1010 to 1111 (ie, the hexadecimal number is 0AH to 0FH) Between the two, you need to add 6 to correct; if you add, the position produces a carry, you also need to add 6 to correct. The reason for this is that the machines are added in binary, so when the 4-bit binary numbers are added, the operation is performed according to the principle of “every sixteen into oneâ€, and essentially two decimal numbers are added, which should be pressed “ The principle of “ten into one†is added, and the difference between 16 and 10 is 6, so when the sum exceeds 9 or there is a carry, add 6 to correct. The following is an example.
An example of a BCD code calculation value needs to be corrected.
(1) Calculate 5+8;
(2) Calculate 8+8
Solution: (1) Enter 5 and 8 into the machine with 8421 BCD, the operation is as follows:
0 1 0 1
+) 1 0 0 0
1 1 0 1 result is greater than 9
+) 0 1 1 0 plus 6 correction
1 0 0 1 1 13 BCD code
The result is 0011, which is a decimal number of 3, and a carry is also generated. 5+8=13, the conclusion is correct.
(2) Enter 8 into the machine with 8421 BCD, and the operation is as follows:
1 0 0 0
+)1 0 0 0
1 0 0 0 0 The result is greater than 9
+)0 1 1 0 plus 6 correction
1 0 1 1 0 16 BCD code
The result is 0110, which is a decimal of 6, and produces a carry. 8+8=16, the conclusion is correct.
Microcomputer principle code: (AL=BCD 5, BL=BCD 8) Let AH=0, then
ADD AL, BL
AAA
The result is AX=0104H, indicating uncompressed decimal number, CF=1, AF=1, AH=1, AL=1
Using the AAA instruction, you can not mask the high nibble, as long as the AAA instruction is executed immediately after the addition, you can get a correct uncompressed decimal number in AX.
The difference between a compressed BCD code and an uncompressed BCD code - each bit of the compressed BCD code is represented by a 4-bit binary, and one byte represents a two-digit decimal number. For example, 10010110B represents a decimal number 96D; an uncompressed BCD code uses 1 byte to represent a decimal number, the upper four bits are always 0000, and the lower 4 bits 0000~1001 represent 0~9. For example, 00001000B represents a decimal number of 8.
Mini Pc I7,Mini Pc I5,Portable Mini Pc,Mini Pc I3
Shenzhen Innovative Cloud Computer Co., Ltd. , https://www.xcypc.com
