The motor is an important actuator for all types of CNC machine tools. To achieve precise position control of the motor, the position of the rotor must be accurately detected. Photoelectric encoders are currently the most commonly used detection devices. Photoelectric encoders are divided into incremental, absolute and hybrid. Among them, the incremental type has been widely used because of its simple structure, long mechanical life, and easy realization of high resolution. Incremental photoelectric encoder output has A, B, Z three-phase signals, in which phase A and phase B are 90° out of phase, Z phase is the “zero position†of the encoder, and only one pulse is output per revolution. In applications, it is often necessary to divide the A-phase and B-phase orthogonal pulses by a certain ratio, that is, a sub-weekly ratio. The difficulty of frequency division is that whether the set sub-week ratio is an integer or a fraction, the A' phase of the output after frequency division, the B' phase pulse still has to be orthogonal or nearly orthogonal. To this end, an FPGA-based integer-to-period ratio implementation method is proposed. The method has simple logical structure, flexible configuration, easy expansion, and high practical value.
1 Electronic gear ratio and weekly ratio The electronic gear ratio and the weekly ratio are a very important concept in CNC machine tools and CNC machining centers. Most of the foreign servo drive devices have an electronic gear ratio and a weekly ratio function. The electronic gear ratio KEG is the ratio of the pulse amount actually executed by the servo motor to the command pulse amount. The KDF is the servo drive received from the servo motor shaft. The ratio of the pulse amount of the pulse encoder to the amount of pulse actually fed back to the upper servo control system (CNC). In combination with the electronic gear ratio and the division ratio function, the user can easily realize the integer pulse equivalent, thereby avoiding the quantization error in the intermediate calculation, and directly transplanting the code to the number of lines equipped with different motor encoders without modifying the G code or Machine tools or machining centers with different pitch screws.
The electronic gear ratio and the division ratio can be calculated by the following equation.
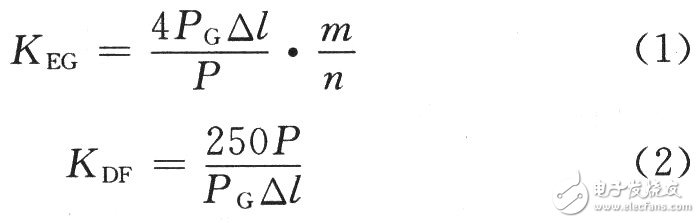
Where: PG is the number of motor photoelectric encoder lines, the unit is P/rev (pulse / revolution); P is the screw pitch, the unit is mm / rev (mm / week); â–³ l is the pulse equivalent, the unit is mm / P (mm/pulse); m/n is the reduction ratio.

The electronic gear ratio can be realized by the transformation of the pulse frequency. For the sub-circumference ratio, since the pulse amount fed back to the CNC by the driver generally adopts an orthogonal pulse sequence, the implementation of the sub-peripheral ratio is difficult with respect to the gear ratio. Various foreign drivers generally have a function of sub-weekly ratio. The research and discussion on the use of FPGA to achieve the weekly ratio, the electronic gear ratio, the function of the weekly ratio is shown in Figure 1.
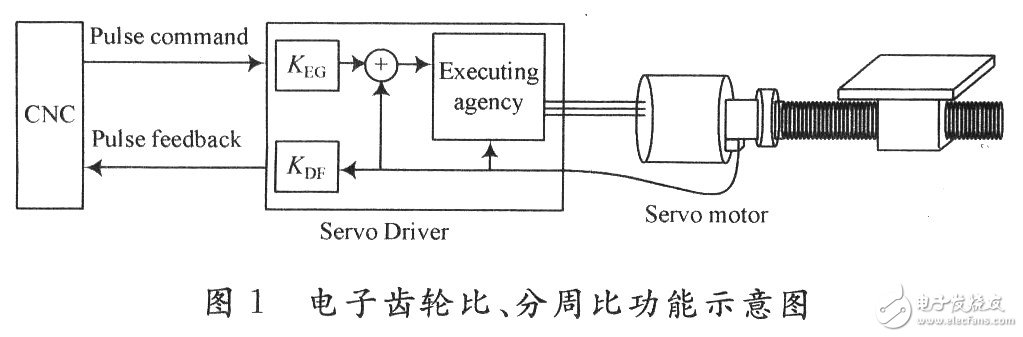
The implementation structure of the weekly ratio function is shown in Figure 2.

The implementation of the weekly ratio requires three functional modules: the quadruple frequency module QD-PF, the frequency division module DF, and the orthogonal sequence generation module OSG. The input of the QDPF module is a quadrature pulse train, and the output is a direction signal and a pulse after quadruple frequency. The DF module can divide the input pulse by three. Inside the DF is an up/down counter that increments and decrements according to the input direction signal. It outputs a pulse and a positive direction signal after the positive value is set to the positive threshold, and outputs a pulse and a negative direction to the set negative threshold. Negative direction signal. When the count value is between the positive and negative thresholds, the output direction signal remains unchanged even if the motor direction changes or even jitters.
The OSG module uses the input pulse edge to trigger the internal state machine to perform state transition, and determines the state to jump according to the input direction signal, thereby generating a quadrature signal and a direction signal.
According to Figure 2, using ACEL's Libro 8.1 development platform, the corresponding functional modules were created using the VHDL hardware language. The schematic diagram is shown in Figure 3.
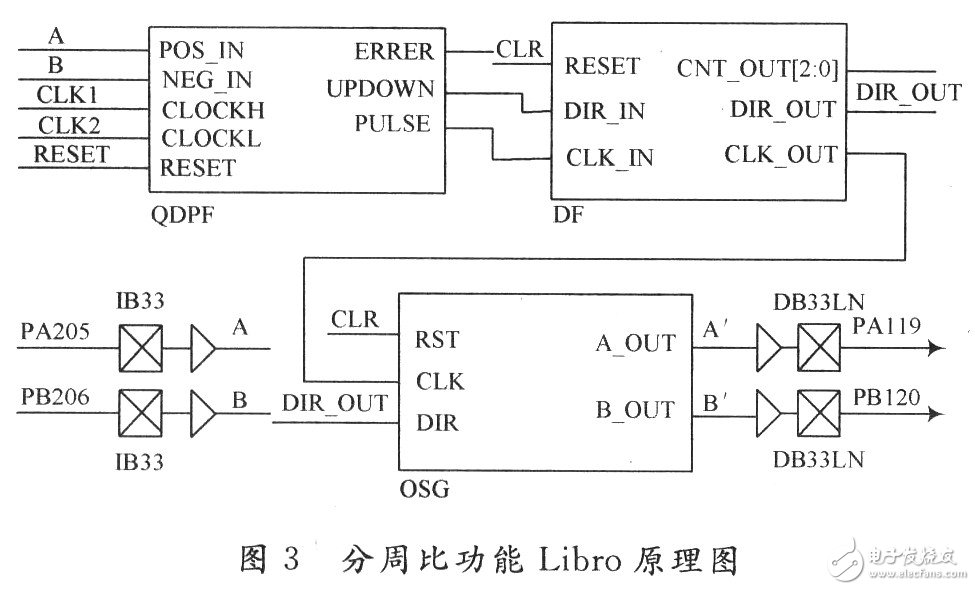
In Fig. 3, PA205 and PB206 are input pins of phase A and phase B of the original differential signal, respectively. After the signal is quadrupled by QDPF, the direction signal and the pulse signal are output to the DF frequency dividing module. After frequency division by DF, the pulse and direction signals are output to the orthogonal pulse generation module OSG to generate a quadrature signal with phase, and finally fed back from the PA119 and PB120 to the CNC.
The main modules are described separately below.
Quadruple Frequency Module QDPF: There are many quadruple frequency methods for quadrature signals, which are covered in many materials and will not be described in detail here.
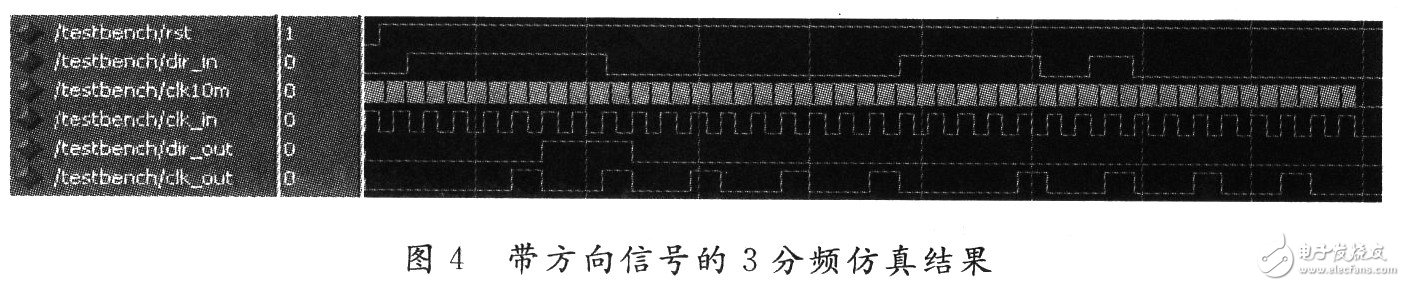
The frequency dividing module DF divides the pulse sequence of the input CLK_IN pin according to the divided ratio of the initial configuration or the preset divided ratio. The internal up/down counter increments the input pulse according to the direction signal input to the DIR_IN pin (DIR_IN=1) or subtracts (DIR_IN=0), and outputs a pulse and positive direction signal (DIR_OUT=1) when counting up to the positive threshold. The count down to the negative threshold is to output a pulse and a negative direction signal (DIR_OUT = 0). If the count value is between the positive and negative thresholds, the output direction signal remains unchanged regardless of the motor reverse or the jitter at the threshold, ie the direction changes repeatedly. This is the key to correctly achieve the crossover. If this step is not handled well, there may be a situation in which the CNC is continuously pulsed after the motor is positioned. Take the three-way frequency as an example, that is, the counter increments to 3 and outputs a positive pulse (positive direction signal + pulse). The counter counts down to -3 and outputs a negative pulse (negative direction signal + pulse). When the count value is (-3, 3), the counter only counts the pulses and does not output them. The simulation results for QDPF are shown in Figure 4.
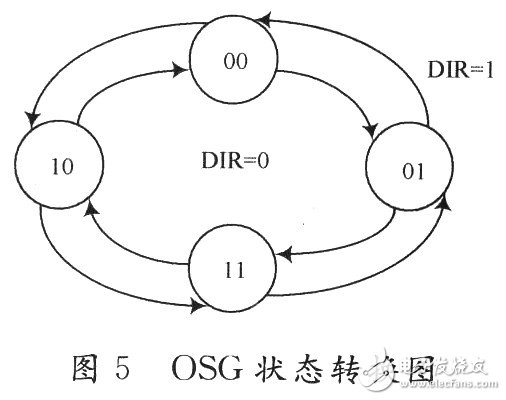
After the OSG is triggered by the rising edge of the pulse signal, it jumps to the next state according to the current state and direction signals. When the direction signal is positive, the state is switched counterclockwise according to the outer ring, and the orthogonal pulse sequence of the A' phase leading the B' phase by 90° is generated; when the direction signal is negative, the state is switched according to the clockwise direction of the inner ring. The orthogonal pulse sequence of the B' phase leading the A' phase by 90° is generated, and the simulation is as shown in 6.
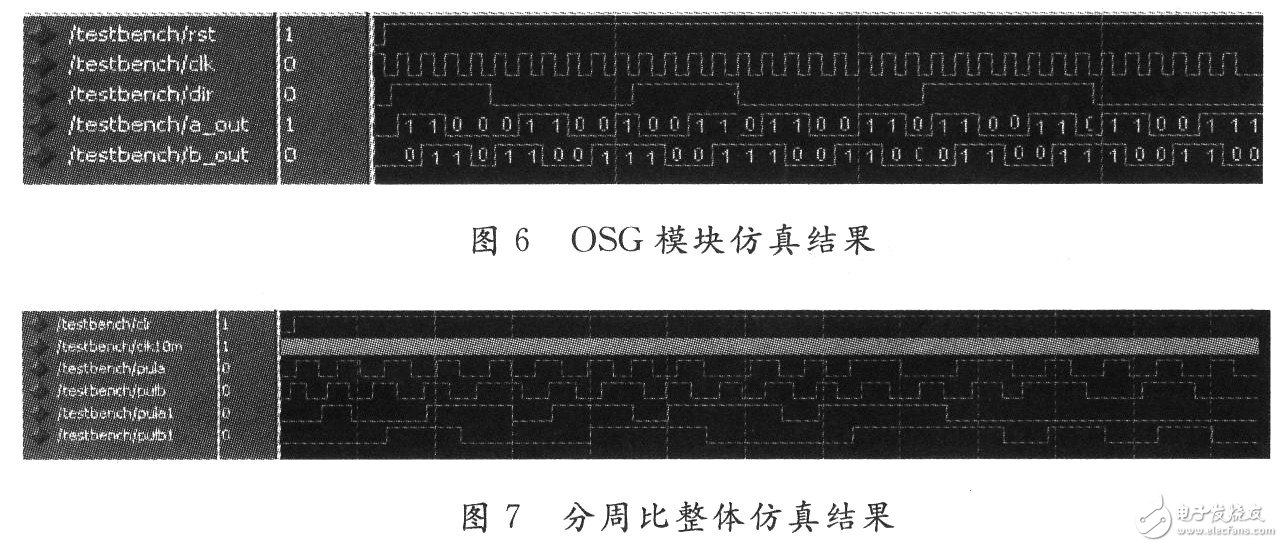
In Figure 6, dir is the direction signal, and its transition edge changes direction. It can be seen from Fig. 6 that the order of the motor forward rotation is 10→11→01→00 (reverse)→01→11→10→.... The phase is switched with the input signal.
Finally, the overall structure of the sub-weekly function is simulated, and the input is an orthogonal pulse sequence. The input simulates the actual motor photoelectric encoder pulse output to repeatedly switch the pulse phase to verify the output of the motor after positioning. The simulation is shown in Figure 7. As can be seen from Fig. 7, when the input signal pula, pulb phase is continuously switched, the output pula1, pulb1 is divided by 3, and 3 or -3 is satisfied, and a new orthogonal sequence is output. The actual experimental waveform is shown in Figure 8.
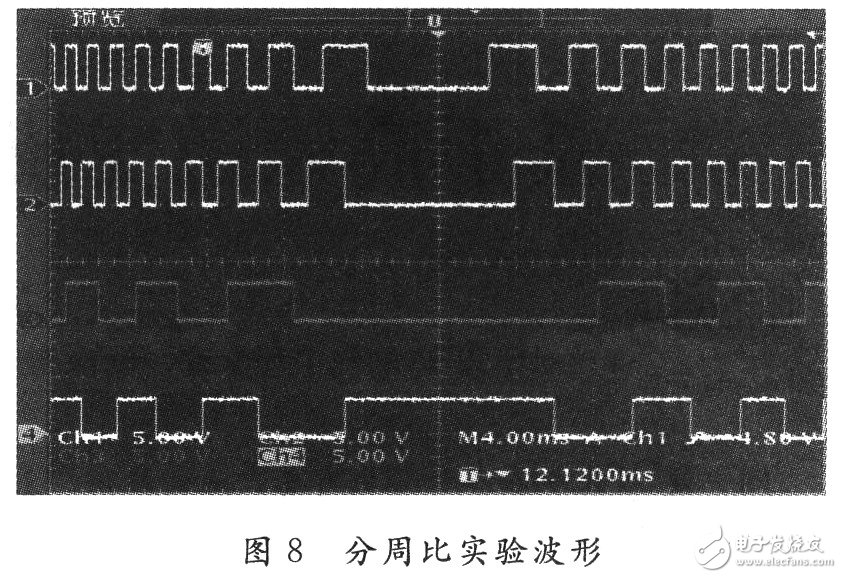
In Fig. 8, waveform 1 and waveform 2 are A-phase and B-phase orthogonal pulses output by the photoelectric encoder, respectively. Waveform 3 and waveform 4 are A' phase and B' phase orthogonal pulses which are divided by A phase and B phase orthogonal pulse 3, respectively. Looking at Figure 7, Figure 8, the results are consistent. The weekly ratio achieved by this scheme has been successfully applied to high-precision servo drivers, and it has been repeatedly verified in practical applications, and no error has been found.
4 ConclusionThe sub-weekly implementation method proposed in this paper can accurately divide the quadrature signal output by the photoelectric encoder according to the set sub-peripheral ratio. By setting the division ratio, it is possible to achieve a frequency division of 1 to 256 times, or even higher. In the actual system, the MCU can also be used to configure the weekly ratio on the bus. If you want to achieve a fractional percentage of the weekly ratio, you only need to improve a little on the basis of this program.
Electrical Meter Sockets,LCD Power Meter Socket,Digital Power Meter Socket,Power Meter Plug Socket
NINGBO COWELL ELECTRONICS & TECHNOLOGY CO., LTD , https://www.cowellsockets.com
