Abstract: This paper introduces the working principle of a millimeter wave velocity radar system. The system uses high-precision spectral analysis method to measure the velocity curve of the outer ballistic projectile, and uses the least squares fitting method to launch the initial velocity of the projectile. The relationship between speed measurement error, accuracy and number of measuring points and extrapolation step size is analyzed. The system successfully applies millimeter wave technology to the testing of internal and external ballistic parameters of artillery or firearms. By comparing with similar products in foreign countries, it is proved that the system has high test accuracy.
Keywords: millimeter wave radar, initial velocity, spectral analysis
With the advancement of weapon testing technology, traditional speed measurement techniques, such as target ring test, sky screen target test and other methods, due to the cumbersome test process and poor precision, can not meet the needs of real-time field test. The millimeter wave speed radar successfully applies the millimeter wave technology to the test of the internal and external ballistic parameters of the artillery or gun. Compared with the existing various speed measuring radars, the millimeter wave speed measuring radar is small in size and light in weight. It is reliable in operation in the test of internal and external ballistics, simple in testing, fast, accurate, and easy to operate. The determination of the initial velocity of the artillery is also It can be used to predict the initial velocity of the artillery, which is of great significance for improving the accuracy of the firing of the artillery.
1 Speed ​​radar system structure and working principleThe millimeter wave speed measuring radar system is mainly composed of a high frequency head [1], a preprocessing system, a terminal system and an infrared starter, and its principle structure is shown in FIG.
The millimeter wave oscillator generates millimeter wave (8mm) oscillation, and its frequency is f0. It is added to the circulator through the isolator, then radiated by the antenna, and propagates in the space as electromagnetic wave. When the electromagnetic wave encounters the target in space ( The bullets are reflected back. If the target is moving, the reflected electromagnetic wave frequency is supplemented by a Doppler frequency fd proportional to the target moving velocity vr, so that the reverse echo frequency becomes f0±fd (the target approaches flight "+", the target Far away from the flight "%"), this echo is received by the antenna, added to the mixer via the circulator, and mixed with the signal leaked by the circulator (as the local oscillator signal) f0 in the mixer. The mixer is a nonlinear component, and its output has a variety of and difference frequencies, such as fd, f0±fd, 2f0±fd, ..., etc., the preamplifier selects the frequency of the Doppler signal (frequency is fd), and then Long cable (length 50 ~ 100m) is sent to the main amplifier of the pre-processing system, the main amplifier is equipped with automatic gain control and manual gain control circuit. Manual gain is used to adjust the overall gain of the amplifier, and automatic gain control is used to increase the dynamic range of the amplifier.
Internal ballistic testing generally does not use automatic gain control. Automatic gain control is only suitable for testing external ballistics, because in the external ballistic test, in order to avoid the interference of the muzzle flame, etc., the appropriate delay should be made to start the test.
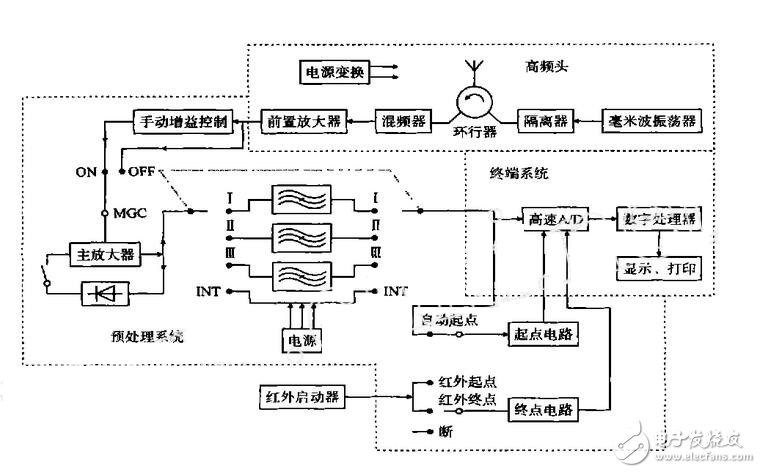
Figure 1 Schematic diagram of the millimeter wave speed radar system
The Doppler signal is amplified by the amplifier and sent to the bandpass filter. If the internal ballistic test is performed, the switch is placed in the all-pass (INT) position, and the signal is sent to the high-speed sampling ADC of the terminal system, and the result is sent to the cache area. The internal ballistics l2t and v2t curves are calculated by the digital processor. If the external ballistic test is performed, the discrete signal is truncated 32 times, and the spectrum of each truncation is obtained. According to the trajectory formed by the main spectrum, the velocity curve of the projectile can be obtained, and then the least squares method is obtained according to the curve. Fit, push out the outer ballistic initial velocity v0 and give the v2t curve. The start and end circuits ensure that the test is performed at the correct time and gives the time base for the test. The internal ballistic test generally uses an automatic starting point and the end point signal can be given by an infrared starter. In the external ballistic test, the starting point signal can use the automatic starting point, and the infrared starter signal can also be used as the starting point. The outer ballistic test generally does not set the end point signal.
Principle of speed measurement for 2 mm wave velocity radar2.1 Principle of speed measurement
As mentioned above, the principle of speed measurement of millimeter wave speed radar is to use the electromagnetic wave to generate Doppler effect when it encounters moving targets in space. That is, the electromagnetic wave (frequency f0) emitted by the radar encounters the echo signal generated by the moving target, the frequency is f0±fd, and fd is the Doppler frequency, which is related to the target radial velocity vr as fd=[2vr/ (c+vr)]f0. where c is the speed of light, generally cμvr. Thus, vr=(λ0/2)fd, where λ0=c/f0 is the wavelength at which electromagnetic waves are emitted. It can be seen that as long as fd is measured (f0 and c are known), the radial velocity vr can be obtained from the equation.
There are roughly two methods for measuring fd: time domain method and frequency domain method. Due to the harsh working environment of the radar (such as the impact vibration of the gun, gun, flame ionization, etc.), the "background" of the received Doppler signal is very complicated, the signal-to-noise ratio is greatly reduced, and the traditional time domain processing method is adopted. It is often difficult to detect or identify Doppler signals that are submerged in interference and noise, resulting in a significant decrease in frequency accuracy. By using the frequency domain spectrum analysis method, selecting the appropriate sampling frequency and appropriate window can greatly improve the frequency measurement accuracy and reliability.
2.2 The basic principle of extrapolation of initial velocity
The basic principle of extrapolating the initial velocity of the millimeter wave velocity radar is to measure the velocity of the projectile at a certain point in the beginning of the outer ballistics (such as t1 to tm), and then push out the initial velocity v0 according to the external ballistic law.
According to the external ballistic theory, at the beginning of the outer ballistics, the velocity can be expressed as v(t)=v0+αt+βt2. Among them, v0 is the initial velocity of the projectile, and α and β are the coincidence coefficients.
The speeds v1, v2, ..., vm measured at times t1, t2, ..., tm are expressed as vi = v0 + αTI + βt2 i + εi, i = 1, 2, ..., m, where εi is a random measurement The error [2] is a random variable, v0, α, β are the parameters to be determined, and v0 is the required initial velocity. According to the least squares method, a set of parameters ^v0, ^α, ^β is obtained, so that the sum of squared residuals of the velocity measurement values ​​Q= ∑ mi=1 [vi -(^v0+^αTI+^βt2i)]2 is the smallest. To this end, the following is derived:
From 5Q/5v0=0,5Q/5α=0,5Q/5β=0, you can get:
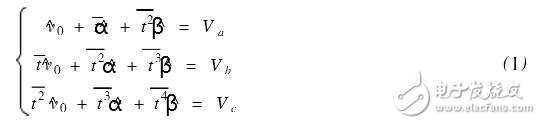
In the formula,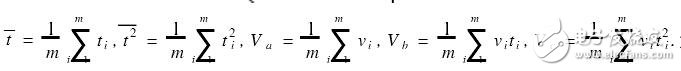 
. Writing (1) as a matrix form is:
S^θ=B
In the formula,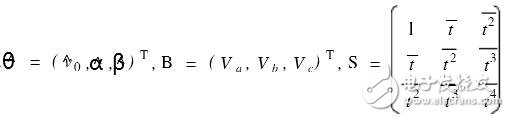 
.
Solving equation (2) gives: ^θ=S -1 B.
When the random variables qi are independent of each other and obey the normal N(0, σ2) distribution, the least squares estimate ^θ will have the following excellent statistical properties, namely (1)^θ is an unbiased estimate of θ; (2) ^θ is the minimum variance estimate of θ; (3) VAR(^θ)=(σ2/m)S-1. Unbiased states that the statistical average of multiple estimates is close to the true value. The minimum variance means that in various estimates, this estimate minimizes the variance, and a small variance means that the estimate deviates from the true value to a lesser extent. Therefore, the size of VAR(^θ) can be used as a criterion for the quality of ^θ. Let C=S-1/m correspond to the deviation E(^v0-E^v0)=C11σ2 of ^v0, where C11 is the corresponding element in matrix C. For the convenience of analysis and calculation, the interval between the measurement points is equidistant, that is, t2-t1=t3-t2=...=tm-tm-1=Tz, and t1=αpTz=Ty, then the elements in the matrix S become ???? t=Z1Tz,t2 =Z2T2 z,t3 =Z3T3z,t4=Z4T4z. where Z1=αp+(m-1)/2, Z2=α2p+αp(m-1)+(m-1)(2m-1 /6, Z3=α3p+3α2p(m-1)/2+αp(m-1)(2m-1)/2+m(m-1)2/4, Z4=α4p+2α3p(m-1 +α2p(m-1)(2m-1)+αpm(m-1)2+(m-1)(2m-1)(3m2-3m-1)/30. Inverting the matrix according to linear algebra The method can be obtained:
It can be seen that the variance E(^v0-E^v0)=C11σ2 of the estimated value ^v0 is related to αp and m, and different αp and m have different variances. The smaller the variance, the better, usually compared with the variance of the error εi of the measured data, so η0=E[^ v0-E^v0]2/σ2 = C11 is defined as the variance compression coefficient of the initial velocity v0. When η0>1, it indicates that the error of extrapolation initial velocity is greater than the measurement error; when η0=1, it indicates that the extrapolation initial velocity error is equal to the measurement error; when η0<1, it indicates that the extrapolation initial velocity error is smaller than the measurement error. It can be seen from the foregoing relationship that η0=C11 is only related to the extrapolation step size αp and the number of measurement points m, so that the required extrapolation precision can be achieved by selecting αp and m. Table 1 shows the number m of measurement points corresponding to the unsynchronized length αp when η0≈1. It can be seen from the table that the larger the extrapolation step αp, the more the number of required points. The millimeter wave speed measuring radar usually takes m=32. At this time, if η0≤1, αp≤6 can be obtained. For example, when the measuring point interval is about 5ms, the delay time is less than 30ms to ensure the accuracy of the extrapolation initial velocity. The measuring point is of equal precision.
If m=32, the relationship between the extrapolation step size αp and the variance compression coefficient η0 of the extrapolation v0 can be calculated according to the above formula, as shown in Table 2.
It can be seen that from the viewpoint of improving the extrapolation accuracy, it is hoped that αp is smaller (m has been determined), that is, the delay time t1 is shorter, but t1 cannot be made too short, otherwise the influence of the mouth flame and the impact vibration cannot be avoided. . According to the actual test needs, the speed measuring radar can be installed on the cradle of the artillery. The observation direction of the radar is consistent with the flying direction of the projectile, and there is no angle correction. If it is erected on a tripod, the observation direction of the radar at this time has a certain angle γ with the direction of the projectile. The speed measured by the radar is only the velocity of the projectile velocity in the γ direction, as shown in Fig. 2. In order to reduce this speed measurement error, D should be minimized and L increased (ie, the delay time t1 is increased).
In order to reduce this speed error, the millimeter wave speed radar generally takes D=0.2~0.5m, L≥25D, and there are L ≈v0t1, v′0=v0/cosγ, γ=arctan(D/L), speed measurement. The relative error σ = (v0 - v'0) / v0 = 1 - v'0 / v0 = 1-v0cos γ / v0 = 1 - cos γ. For example, to test a 7.62mm rifle, D=0.2m, and set the initial velocity v0=760m/s, then t1≥L/v0≥25&TImes;0.2/760=6158ms. Take t1=7ms, then the speed measurement accuracy is σ =1-cos[arctan(D/L)]=1-cos{arctan[012/(760&TImes;7×10-3)]}=711×10-4.
3 ConclusionThe millimeter wave speed measuring radar has been successfully applied to many domestic shooting ranges, and its testing accuracy is 0.1%. The test results are consistent with the foreign 582 radar and the Danish Weibulel radar. In practical applications, it is found that the delay time parameter of the data acquisition (extrapolation step size) has the same effect on the accuracy of the initial velocity value of the test, but the setting of the extrapolation step is also related to many other factors, such as it varies. The type of bomb, the ambient temperature, etc. vary. The mechanism and related theory for delay time selection need further research or a large number of experimental demonstrations to further improve the test accuracy.
references:1 Meng Qingyu, Lu Shiliang. Eight-mm microstrip Doppler radar transceiver front-end. Journal of Hefei University of Technology, 1995, 18(3): 98-101
2 Buildings, radar accuracy analysis. Beijing: National Defense Industry Press, 1979
Introducing the reliable and efficient LiFePO4 Cell, with a nominal voltage of 3.2V, perfect for powering your devices and equipment with ease. These cells are designed with advanced technology, ensuring a stable and consistent power supply to your devices. The Lithium Iron Phosphate (LiFePO4) chemistry used in these cells makes it the perfect choice for high-performance applications. These cells have excellent discharge characteristics and a long life cycle, making them a cost-effective and eco-friendly option.
Lifepo4 Cell,Lifepo4 Battery,Lithium Iron Battery,Cylindrical Lifepo4 Battery
JIANGMEN RONDA LITHIUM BATTERY CO., LTD. , https://www.ronda-battery.com