A very simple compression method is run length encoding, which replaces the same continuous data with a simple encoding such as data and data length, which is an example of lossless data compression. This approach is often used in office computers to make better use of disk space or to make better use of bandwidth in computer networks. For symbolic data such as spreadsheets, texts, executables, etc., losslessness is a very critical requirement because, except for a limited number of cases, even a single bit of data change is unacceptable in most cases.
For video and audio data, a certain degree of quality degradation is acceptable as long as no significant loss of data is important. By utilizing the limitations of the human perception system, significant savings in storage space can be achieved and the quality of the resulting results is not significantly different from the raw data quality. These lossy data compression methods typically require a compromise between compression speed, compressed data size, and quality loss.
Lossy image compression is used in digital cameras, which greatly improves storage capacity while reducing image quality. The lossy MPEG-2 codec video compression for DVD also implements similar functionality.
In lossy audio compression, psychoacoustic methods are used to remove components that are inaudible or difficult to hear in the signal. The compression of human speech often uses more specialized techniques, so people sometimes distinguish "voice compression" or "voice coding" from "audio compression" as an independent research field. Different audio and speech compression standards fall into the category of audio codecs. For example, voice compression is used for Internet telephony, and audio compression is used for CD dubbing and decoding using an MP3 player.
Compression is the process of converting data into a more compact form than the original format in order to reduce storage space. The concept of data compression is quite old and can be traced back to the mid-19th century when Morse code was invented.
The invention of Morse code is to enable telegraphers to transmit letter messages through a telegraph system using a series of audible pulse signals to transmit text messages. The inventors of Morse code realized that some letters were used more frequently than others (for example, E is more common than X), so it was decided to use short pulse signals to represent common letters, and longer pulse signals were used. letter. This basic compression scheme effectively improves the overall efficiency of the system because it allows the telegrapher to transmit more information in less time.
Although modern compression processes are much more complicated than Morse code, they still use the same basic principles, which are what we will cover in this article. These concepts are critical to the efficient operation of our computer world today—everything on the Internet from local and cloud storage to data flow relies heavily on compression algorithms, and leaving it is likely to become very inefficient.
Compressed pipe
The following figure shows the general flow of a compression scheme. The raw input data contains a sequence of symbols that we need to compress or reduce. These symbols are encoded by the compressor and the output is encoded data. It should be noted that although the encoded data is usually smaller than the original input data, there are exceptions (which we will discuss later).
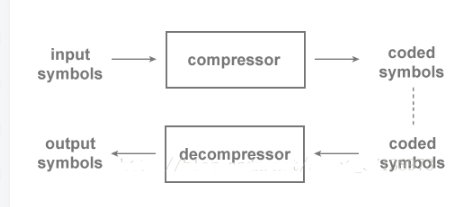
Usually at some later time, the encoded data is input to a decompressor where the data is decoded, reconstructed, and the raw data is output as a sequence of symbols. Note that in this article we will alternately use "sequence" and "string" to refer to a sequence of symbol sequences.
If the output data and the input data are always identical, then this compression scheme is called lossless, also known as lossless encoder. Otherwise, it is a lossy compression scheme.
Lossless compression schemes are often used to compress text, executable programs, or any other place where data needs to be completely rebuilt.
Lossy compression schemes are useful in images, audio, video, or other situations where information loss can be accepted to improve compression efficiency.
Data model
Information is defined as the amount by which the complexity of a piece of data is measured. The more information a data set has, the harder it is to be compressed. The concept of rare concepts and information is relevant because the appearance of rare symbols provides more information than the appearance of common symbols.
For example, the “earthquake in Japan†appeared less than the “earthquake in the moon†because the earthquake on the moon was very uncommon. We can expect that most compression algorithms will carefully consider the frequency or probability of occurrence of a symbol when it is compressed.
We use the compression algorithm to reduce the effectiveness of the information load, called its efficiency. A more efficient compression algorithm can reduce the size of a particular data set more than an inefficient compression algorithm.
Probability model
The most important step in designing a compression scheme is to create a probabilistic model for the data. This model allows us to measure the characteristics of the data to achieve an effective adaptation to the compression algorithm. To make it clearer, let's take a look at some parts of the modeling process.
Suppose we have an alphabet G that consists of all the characters that may appear in the dataset. In our example, G contains 4 characters: from A to D.
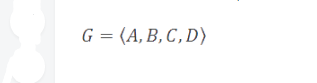
We also have a probability statistical function P that defines the probability of each character appearing in G in the input data string. In the input data string, symbols with high probability are more likely to appear than symbols with lower probability.

In this example, we assume that the symbols are independently and identically distributed. In the source data string, the appearance of a symbol has no correlation with any other symbol.
Minimum coding rate
B is the most common symbol, and the probability of occurrence is 40%; and C is the least common symbol, and its probability of occurrence is only 10%. Our goal is to design a compression scheme that minimizes the required storage space for common symbols, while it supports the use of more necessary space to store uncommon symbols. This trade-off is the basic principle of compression and is already present in almost all compression algorithms.
With the alphabet, we can try to define a basic compression scheme. If we simply encode a symbol into an 8-bit ASCII value, then our compression efficiency, ie the coding rate, will be 8 bits/symbol. Suppose we improve this scheme for an alphabet that only contains 4 symbols. If we assign 2 bits to each symbol, we can still completely reconstruct the encoded data string, and only need 1/4 of the space.
ASCII
In the computer, all data is stored in binary numbers (because the computer uses high and low levels to represent 1 and 0, respectively), for example, 52 letters like a, b, c, d (including uppercase), and 0, 1 and other numbers and some commonly used symbols (such as *, #, @, etc.) should also be represented by binary numbers when stored in the computer, and which binary numbers are used to represent which symbols, of course Everyone can agree on their own set (this is called coding), and if you want to communicate with each other without causing confusion, then everyone must use the same coding rules, so the relevant American standardization organization has issued ASCII code. Uniformly stipulates which binary numbers are used to represent the above common symbols.
It is the most versatile single-byte encoding system available today.
At this time, we have significantly improved the coding rate (from 8 to 2 bits/symbol), but completely ignored our probability model. As mentioned earlier, we can invent a strategy in conjunction with the model to use more bits for common symbols (B and D) and more bits for less common symbols (A and C) to improve coding efficiency.
This raises an important point of view in Shannon's pioneering papers—we can simply define its theoretical minimum storage space based on the probability of a symbol (or event). We define the minimum coding rate of a symbol as follows:
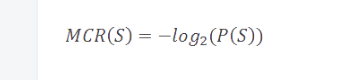
For example, if the probability of a symbol appearing is 50%, then it absolutely needs at least one byte to store.
Entropy and redundancy
Further, if we calculate the weighted average of the minimum coding rate for the characters in the alphabet, we get a value called Shannon Entropy, which is simply called the entropy of the model. Entropy is defined as the minimum coding rate for a given model. It is built on top of the alphabet and its probabilistic model, as described below.
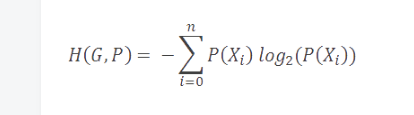
As you might expect, models with more rare symbols have higher entropy than models with fewer and common symbols. Furthermore, models with higher entropy values ​​are more difficult to compress than models with lower entropy values.
In our current example, the entropy value of our model is 1.85 bits/symbol. The difference between the coding rate (2) and the entropy value (1.85) is called the redundancy of the compression scheme.
Entropy is a very useful topic in many different sub-areas such as encryption and artificial intelligence.
Coding model
So far, we have taken a little bit of freedom: automatically giving the probability of our symbols. In reality, models are usually not readily available, and we may obtain these probability values ​​by analyzing source data strings (such as summarizing statistical symbol probabilities in sample data) or adaptively learning during compression. In either case, the probability value of the real data string does not perfectly match the model, and we will lose compression efficiency proportionally to this difference. For this reason, it is crucial to derive (or constantly maintain) a model that is as accurate as possible.
Common algorithm
When we define the probability model for the data set, we can use this model to design a compression scheme. Although the process of developing a new compression algorithm is beyond the scope of this article, we can take advantage of existing algorithms. Below we review some of the most popular algorithms.
Each of the following algorithms is a sequential processor, which means that if the nth symbol of the encoded sequence is to be reconstructed, it must first be 0. (n-1) symbols are decoded. Due to the indefinite length of the encoded data, the seek operation is not possible - the decoder cannot jump directly to the correct offset position of the symbol n without decoding the preceding symbols. In addition, some coding schemes rely on the internal history state that is maintained as each symbol is processed sequentially.
Huffman coding
This is one of the most widely known compression schemes. It dates back to the 1950s, and David Huffman first described this approach in his paper "A Method of Constructing Very Small Unwanted Encodings." Huffman coding works by getting the optimal prefix code for a given alphabet.
A prefix code represents a value and the prefix code for each symbol in the alphabet does not become a prefix for another symbol prefix code. For example, if 0 is the prefix code for our first symbol A, then the other symbols in the alphabet cannot start with 0. It is useful because the prefix code makes the bitstream decoding clear and unambiguous.
Dictionary method
This type of encoder uses a dictionary to hold recently discovered symbols. When a symbol is encountered, it is first looked up in the dictionary to check if it has been stored. If so, the output will only contain a reference to the dictionary entry (usually an offset) instead of the entire symbol.
Compression schemes using the dictionary approach include LZ77 and LZ78, which are the basis for many different lossless compression schemes.
In some cases, a sliding window is used to adaptively track recently discovered symbols. In this case, a symbol is only saved in the dictionary when it is found relatively close. Otherwise, the symbol is culled (it may re-join the dictionary afterwards). This process prevents the symbol dictionary from becoming too large and takes advantage of the fact that symbols in the sequence will repeat in relatively short windows.
Columbus index code
Suppose you have an alphabet consisting of integers in the range 0 to 255, and the probability of occurrence of a symbol is related to its distance to zero. Thus, smaller values ​​are the most common, and larger values ​​have a lower probability of occurrence.
Like most compression schemes, the efficiency of Columbus encoding relies heavily on specific symbols in the input sequence. Sequences containing many large values ​​are less compressed than sequences containing less large values; in some cases, the Columbus-encoded sequence may even be larger than the original input string.
Arithmetic coding
Arithmetic coding is a relatively new compression algorithm that has gained popularity in recent times (for the past 15 years), especially in terms of media compression. The arithmetic encoder is a highly efficient, computationally intensive, timing encoder.
A common arithmetic coding variant, binary arithmetic coding, uses an alphabet containing only two symbols (0 and 1). This variant is particularly useful because it simplifies the design of the encoder, reduces the computational cost of runtime, and does not require any explicit communication when the encoder and decoder process an alphabet and model.
Run length coding
Until now, we have assumed that the source symbols are independently and identically distributed. Our probability model and the calculation of coding rate and entropy depend on this fact. But what if our symbol sequence does not meet this requirement?
Suppose the repetition of the symbols in our sequence is high, and the appearance of a particular symbol strongly suggests that its repeated instances are about to follow. In this case, we can choose to use another encoding scheme called run length encoding. This technique performs well when the symbol repetition is high, and performs poorly when the repetition is low.
The run length encoder predicts the length of consecutively repeated symbols in the data string and replaces them with this symbol and the number of repetitions.
Perfect fit: The Hydrogel Screen Protector is designed with a Soft TPU material, which can be completely covered even on a curved device, providing perfect protection for the full coverage of the screen.
Oleophobic and waterproof: The use of hydrophobic and oleophobic screen coatings can prevent sweat, grease residue and fingerprints without reducing screen sensitivity. It is almost invisible on the screen and brings a high-definition visual experience.
Sensitive touch: ultra-thin and Soft Hydrogel Film with a thickness of only 0.14mm. As time goes by, it will self-repair minor scratches, provide you with a highly responsive screen protector and maintain the original touch.
Easy to install: The installation of the Protective Film is very simple, without air bubbles. The protective sticker can stay on the phone perfectly, and the bubbles will disappear within 24 hours.
If you want to know more about Hydrogel Screen Protector products, please click the product details to view the parameters, models, pictures, prices and other information about Hydrogel Screen Protective Film.
Whether you are a group or an individual, we will try our best to provide you with accurate and comprehensive information about the Hydrogel Protective Film!
Hydrogel TPU Protective Film,Ultra-Thin Protective Film,Soft Hydrogel Film,Hydrogel Film Screen Protector,Screen Protective Film,Mobile Phone Screen Guards
Shenzhen Jianjiantong Technology Co., Ltd. , https://www.jjthydrogelmachine.com
